# 递归的概念
直接或间接地调用自身的算法称为递归算法。用函数自身给出定义的函数称为递归函数
由分治法产生的子问题往往是原问题的较小模式,这就为使用递归技术提供了方便。在这种情况下,反复应用分治手段,可以使子问题与原问题类型一致而其规模却不断缩小,最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。
分治与递归像一对孪生兄弟,经常同时应用在算法设计之中,并由此产生许多高效算法。
优点:
缺点:
在递归算法中消除递归调用,使其转化为非递归算法。
采用一个用户定义的栈来模拟系统的递归调用工作栈。该方法通用性强,但本质上还是递归,只不过人工做了本来由编译器做的事情,优化效果不明显。
用递推来实现递归函数。
通过变换能将一些递归转化为尾递归,从而迭代求出结果。
# 分治的基本思想分治法的基本思想是将一个规模为 n 的问题分解为 k 个规模较小的子问题,这些子问题相互独立且与原问题相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解
# 分治法的适用条件分治法所能解决的问题一般具有以下几个特征:
该问题的规模缩小到一定的程度就可以容易地解决;
该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质
利用该问题分解出的子问题的解可以合并为该问题的解;
该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
# 代码框架代码框架 1 2 3 4 5 6 7 8 9 divide-and-conquer(P) { if ( | P | <= n0) adhoc(P); divide P into smaller subinstances P1,P2,...,Pk; for (i=1 ,i<=k,i++) yi=divide-and-conquer(Pi); return merge(y1,...,yk); }
# 求解递归# 猜测法用于验证
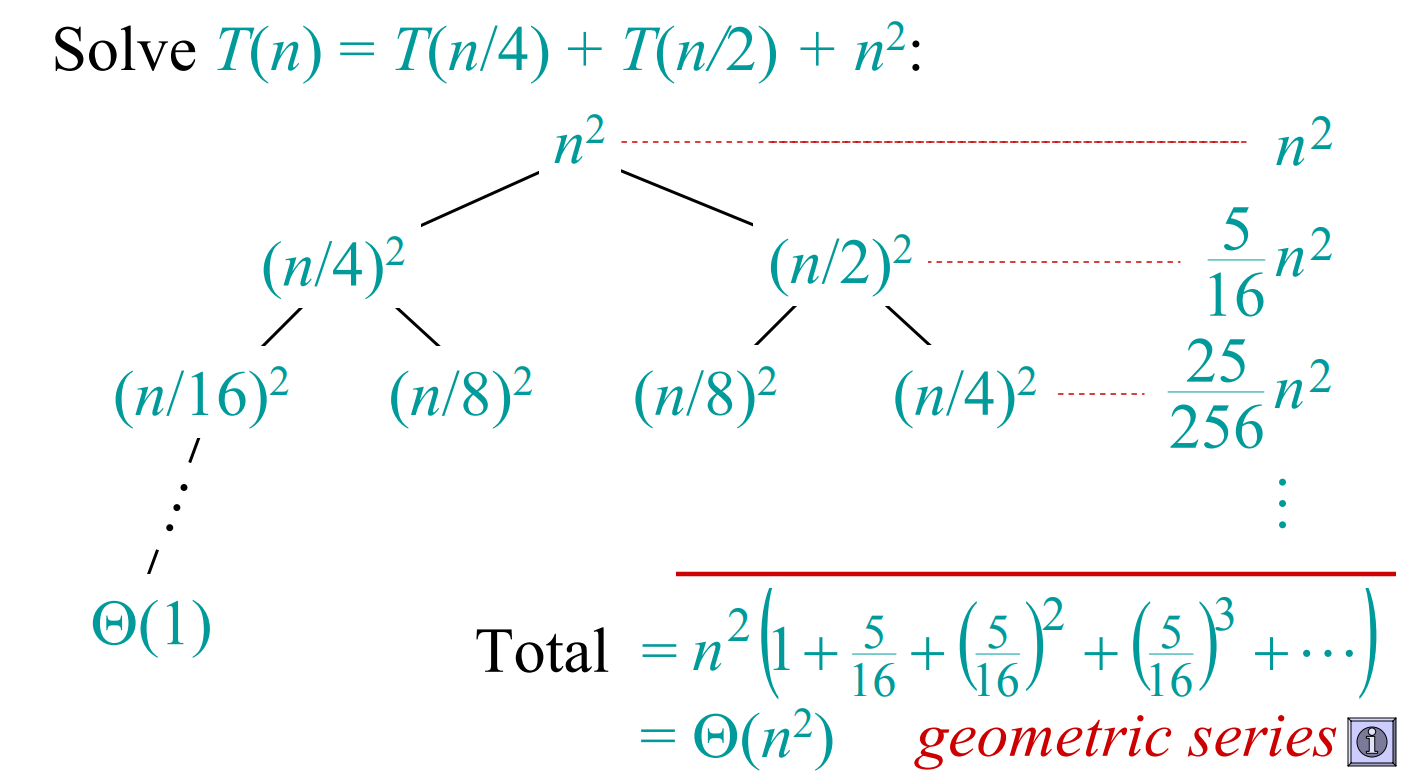
# 递归树法n 2 n^2 n 2 n 2 n^2 n 2
# 递归树法例题
T ( n ) = 3 T ( n / 4 ) + c n 2 T (n) = 3T (n/4) + cn^2 T ( n ) = 3 T ( n / 4 ) + c n 2
解答
每分解一层,代价为c n 2 cn^2 c n 2 h = l o g 4 n h=log_4n h = l o g 4 n 3 h 3^h 3 h n l o g 4 3 n^{log_43} n l o g 4 3
T ( n ) = 3 T ( n / 4 ) + c n 2 = c n 2 + 3 16 c n 2 + ( 3 16 ) 2 c n 2 … = ∑ i l o g 4 ( n − 1 ) ( 3 16 ) i c n 2 + Θ ( n l o g 4 3 ) < ∑ i ∞ ( 3 16 ) i c n 2 + Θ ( n l o g 4 3 ) = 1 1 − 3 / 16 c n 2 + Θ ( n l o g 4 3 ) = O ( n 2 ) T (n) = 3T (n/4) + cn^2\\ = cn^2+\frac{3}{16}cn^2+(\frac{3}{16})^2cn^2\dots \\ =\displaystyle \sum^{log_4(n-1)}_i(\frac{3}{16})^icn^2+\Theta(n^{log_43})<\displaystyle \sum^{\infin}_i(\frac{3}{16})^icn^2+\Theta(n^{log_43})\\ =\frac{1}{1-3/16}cn^2+\Theta(n^{log_43})\\ =O(n^2) T ( n ) = 3 T ( n / 4 ) + c n 2 = c n 2 + 1 6 3 c n 2 + ( 1 6 3 ) 2 c n 2 … = i ∑ l o g 4 ( n − 1 ) ( 1 6 3 ) i c n 2 + Θ ( n l o g 4 3 ) < i ∑ ∞ ( 1 6 3 ) i c n 2 + Θ ( n l o g 4 3 ) = 1 − 3 / 1 6 1 c n 2 + Θ ( n l o g 4 3 ) = O ( n 2 )
T ( n ) = T ( n / 3 ) + T ( 2 n / 3 ) + c n T(n) = T (n/3) + T (2n/3) + cn T ( n ) = T ( n / 3 ) + T ( 2 n / 3 ) + c n
解答
每分解一层,代价为c n cn c n h = l o g 3 / 2 n h=log_{3/2}n h = l o g 3 / 2 n c n cn c n
$T(n) = T (n/3) + T (2n/3) + cn\ <cnlog_{3/2}n \ =O(nlgn) $
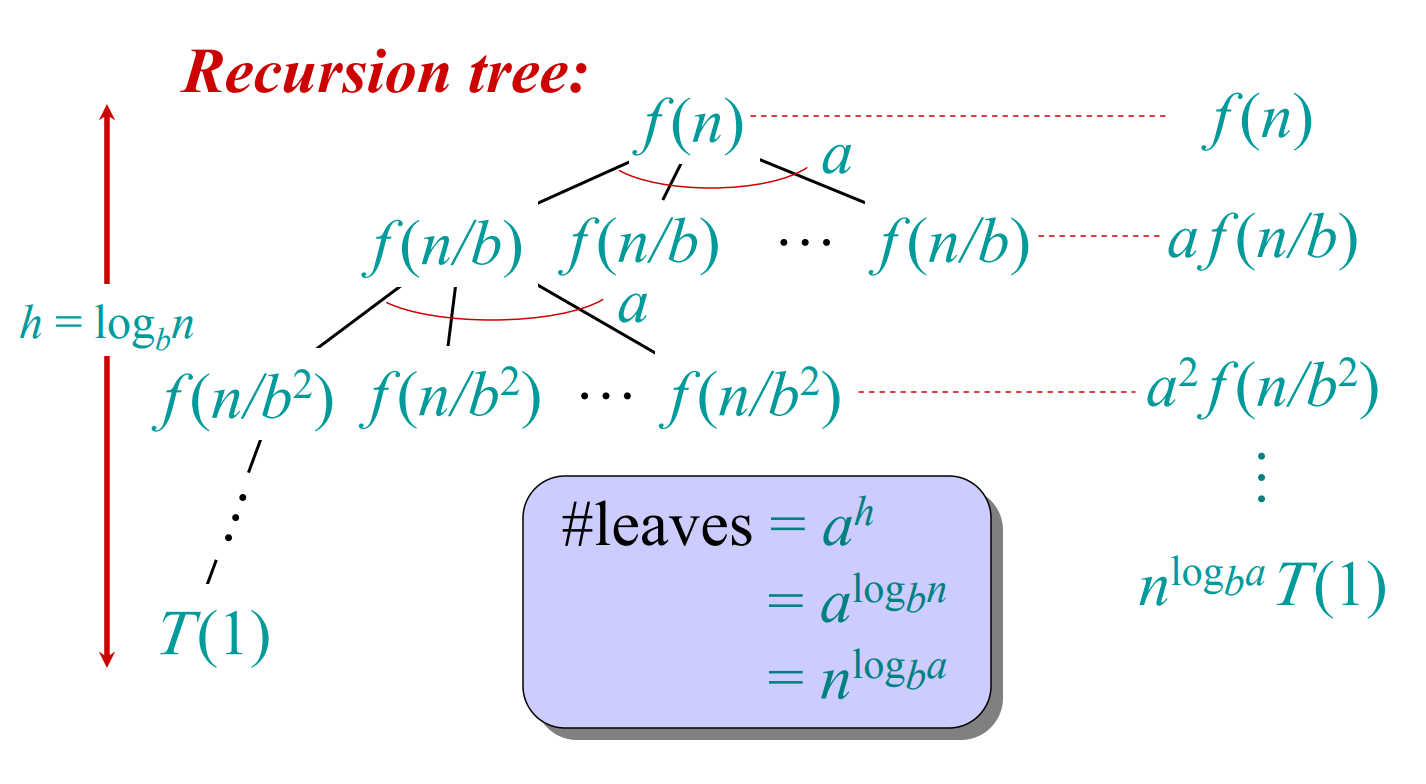
# 主方法T ( n ) = a T ( n / b ) + f ( n ) T(n)=aT(n/b)+f(n) T ( n ) = a T ( n / b ) + f ( n ) a ≥ 1 , b > 1 , f a s y m p t o t i c a l l y p o s i t i v e a \geq 1,b> 1,f\ asymptotically\ positive a ≥ 1 , b > 1 , f a s y m p t o t i c a l l y p o s i t i v e c o m p a r e f ( n ) w i t h n l o g b a compare\ f(n)\ with\ n^{log_ba} c o m p a r e f ( n ) w i t h n l o g b a
f ( n ) = O ( n l o g b a − ϵ ) f o r s o m e c o n s t a n t ϵ > 0 f(n)=O(n^{log_ba-\epsilon}) for\ some\ constant\ \epsilon >0 f ( n ) = O ( n l o g b a − ϵ ) f o r s o m e c o n s t a n t ϵ > 0 T ( n ) = Θ ( n l o g b a ) T(n)=\Theta(n^{log_ba}) T ( n ) = Θ ( n l o g b a ) f ( n ) f(n) f ( n ) n l o g b a b y n ϵ n^{log_ba}\ by\ n^\epsilon n l o g b a b y n ϵ f ( n ) = Θ ( n l o g b a l g k n ) f o r s o m e c o n s t a n t k ≥ 0 f(n)=\Theta(n^{log_ba}lg^kn) for\ some\ constant\ k \geq 0 f ( n ) = Θ ( n l o g b a l g k n ) f o r s o m e c o n s t a n t k ≥ 0 T ( n ) = Θ ( n l o g b a l g k + 1 n ) T(n)=\Theta(n^{log_ba}lg^{k+1}n) T ( n ) = Θ ( n l o g b a l g k + 1 n ) f ( n ) f(n) f ( n ) n l o g b a n^{log_ba} n l o g b a f ( n ) = Ω ( n l o g b a + ϵ ) f o r s o m e c o n s t a n t ϵ > 0 f(n)=\Omega(n^{log_ba+\epsilon}) for\ some\ constant\ \epsilon >0 f ( n ) = Ω ( n l o g b a + ϵ ) f o r s o m e c o n s t a n t ϵ > 0 T ( n ) = Θ ( f ( n ) ) T(n)=\Theta(f(n)) T ( n ) = Θ ( f ( n ) ) f ( n ) f(n) f ( n ) n l o g b a b y n ϵ n^{log_ba}\ by\ n^\epsilon n l o g b a b y n ϵ f ( n ) f(n) f ( n ) a f ( n / b ) ≤ c f ( n ) f o r c o s t a n t c < 1 af(n/b)\leq cf(n) \ for \ costant \ c<1 a f ( n / b ) ≤ c f ( n ) f o r c o s t a n t c < 1
# 主方法例题
T ( n ) = 4 T ( n / 2 ) + n T(n)=4T(n/2)+n T ( n ) = 4 T ( n / 2 ) + n
解答
a = 4 , b = 2 ⟹ n l o g b a = n 2 ; f ( n ) = n a=4,b=2\implies n^{log_ba}=n^2;f(n)=n a = 4 , b = 2 ⟹ n l o g b a = n 2 ; f ( n ) = n f ( n ) = O ( n 2 − ϵ ) f o r ϵ = 1 f(n)=O(n^{2-\epsilon})for\ \epsilon=1 f ( n ) = O ( n 2 − ϵ ) f o r ϵ = 1 T ( n ) = Θ ( n 2 ) T(n)=\Theta(n^2) T ( n ) = Θ ( n 2 )
T ( n ) = 4 T ( n / 2 ) + n 2 T(n)=4T(n/2)+n^2 T ( n ) = 4 T ( n / 2 ) + n 2
解答
a = 4 , b = 2 ⟹ n l o g b a = n 2 ; f ( n ) = n 2 a=4,b=2\implies n^{log_ba}=n^2;f(n)=n^2 a = 4 , b = 2 ⟹ n l o g b a = n 2 ; f ( n ) = n 2 f ( n ) = Θ ( n 2 l g 2 n ) , t h a t i s k = 0 f(n)=\Theta(n^2lg^2n),that\ is\ k=0 f ( n ) = Θ ( n 2 l g 2 n ) , t h a t i s k = 0 T ( n ) = Θ ( n 2 l g n ) T(n)=\Theta(n^2lgn) T ( n ) = Θ ( n 2 l g n )
T ( n ) = 4 T ( n / 2 ) + n 3 T(n)=4T(n/2)+n^3 T ( n ) = 4 T ( n / 2 ) + n 3
解答
a = 4 , b = 2 ⟹ n l o g b a = n 2 ; f ( n ) = n 3 a=4,b=2\implies n^{log_ba}=n^2;f(n)=n^3 a = 4 , b = 2 ⟹ n l o g b a = n 2 ; f ( n ) = n 3 f ( n ) = O ( n 2 + ϵ ) f o r ϵ = 1 f(n)=O(n^{2+\epsilon})for\ \epsilon=1 f ( n ) = O ( n 2 + ϵ ) f o r ϵ = 1 a n d 4 ( c n / 2 ) ≤ c n 3 f o r c = 1 / 2 and \ 4(cn/2)\leq cn^3\ for c=1/2 a n d 4 ( c n / 2 ) ≤ c n 3 f o r c = 1 / 2 T ( n ) = Θ ( n 3 ) T(n)=\Theta(n^3) T ( n ) = Θ ( n 3 )
T ( n ) = 4 T ( n / 2 ) + n 2 / l g n T(n)=4T(n/2)+n^2/lgn T ( n ) = 4 T ( n / 2 ) + n 2 / l g n
解答
不适用任何一种情况,因为n ϵ = ω ( l g n ) n^\epsilon=\omega(lgn) n ϵ = ω ( l g n )
# General method(Akra-Bazzi)T ( n ) = ∑ i = 1 k a i T ( n / b i ) + f ( n ) T(n)=\displaystyle \sum ^k_{i=1}a_iT(n/b_i)+f(n) T ( n ) = i = 1 ∑ k a i T ( n / b i ) + f ( n ) ∑ i = 1 k ( a i / b i p ) = 1 \displaystyle \sum ^k_{i=1}(a_i/b_i^p)=1 i = 1 ∑ k ( a i / b i p ) = 1 n p n^p n p n l o g b a n^{log_ba} n l o g b a
# 根据代码判断复杂度的方法
for /while 循环
嵌套循环
顺序语句
if-else 语句
求解递归
赋值
# 分治算法设计与技巧重要知识点# 二分搜索二分搜索 1 2 3 4 5 6 7 8 9 10 template<class Type > int BinarySearch (Type a[], const Type& x, int l, int r) { while (r >= l){ int m = (l+r)/2 ; if (x == a[m]) return m; if (x < a[m]) r = m-1 ; else l = m+1 ; } return -1 ; }
算法复杂度分析:
# 大整数乘法请设计一个有效的算法,可以进行两个 n 位大整数的乘法运算X = a 2 n / 2 + b , Y = c 2 n / 2 + d X = a 2^{n/2} + b ,\ Y = c 2^{n/2} + d X = a 2 n / 2 + b , Y = c 2 n / 2 + d X Y = a c 2 n + ( a d + b c ) 2 n / 2 + b d XY = ac 2^n + (ad+bc) 2^{n/2} + bd X Y = a c 2 n + ( a d + b c ) 2 n / 2 + b d
X Y = a c 2 n + ( ( a − c ) ( b − d ) + a c + b d ) 2 n / 2 + b d XY = ac 2^n + ((a-c)(b-d)+ac+bd) 2^{n/2} + bd X Y = a c 2 n + ( ( a − c ) ( b − d ) + a c + b d ) 2 n / 2 + b d X Y = a c 2 n + ( ( a + c ) ( b + d ) − a c − b d ) 2 n / 2 + b d XY = ac 2^n + ((a+c)(b+d)-ac-bd) 2^{n/2} + bd X Y = a c 2 n + ( ( a + c ) ( b + d ) − a c − b d ) 2 n / 2 + b d
两个 XY 的复杂度都是O ( n l o g 3 ) O(n^{log3}) O ( n l o g 3 ) T ( n ) = { O ( 1 ) n = 1 3 T ( n / 2 ) + O ( n ) n > 1 T(n)=\begin{cases}
O(1)\ n=1\\
3T(n/2)+O(n)\ n>1
\end{cases} T ( n ) = { O ( 1 ) n = 1 3 T ( n / 2 ) + O ( n ) n > 1 T ( n ) = O ( n l o g 3 ) = O ( n 1.59 ) T(n)=O(n^{log3}) =O(n^{1.59}) T ( n ) = O ( n l o g 3 ) = O ( n 1 . 5 9 )
# strassen 矩阵乘法将矩阵 A,B 和 C 中每一矩阵都分块成 4 个大小相等的子矩阵。由此可将方程 C=AB 重写为:[ C 11 C 12 C 12 C 22 ] = [ A 11 A 12 A 12 A 22 ] [ B 11 B 12 B 12 B 22 ] \begin{bmatrix}
C_{11} &C_{12}\\
C_{12}&C_{22}
\end{bmatrix}=
\begin{bmatrix}
A_{11} &A_{12}\\
A_{12}&A_{22}
\end{bmatrix}
\begin{bmatrix}
B_{11} &B_{12}\\
B_{12}&B_{22}
\end{bmatrix} [ C 1 1 C 1 2 C 1 2 C 2 2 ] = [ A 1 1 A 1 2 A 1 2 A 2 2 ] [ B 1 1 B 1 2 B 1 2 B 2 2 ]
C 11 = A 11 B 11 + A 12 B 21 C 12 = A 11 B 12 + A 12 B 22 C 21 = A 21 B 11 + A 22 B 21 C 22 = A 22 B 12 + A 22 B 22
C_{11}=A_{11}B_{11}+A_{12}B_{21}\\
C_{12}=A_{11}B_{12}+A_{12}B_{22}\\
C_{21}=A_{21}B_{11}+A_{22}B_{21}\\
C_{22}=A_{22}B_{12}+A_{22}B_{22}
C 1 1 = A 1 1 B 1 1 + A 1 2 B 2 1 C 1 2 = A 1 1 B 1 2 + A 1 2 B 2 2 C 2 1 = A 2 1 B 1 1 + A 2 2 B 2 1 C 2 2 = A 2 2 B 1 2 + A 2 2 B 2 2
为了降低时间复杂度,必须减少乘法的次数。
M 1 = A 11 ( B 12 − B 22 ) M 2 = ( A 11 + A 12 ) B 22 M 3 = ( A 21 + A 22 ) B 11 M 4 = A 22 ( B 21 − B 11 ) M 5 = ( A 11 + A 22 ) ( B 11 + B 22 ) M 6 = ( A 12 − A 22 ) ( B 21 + B 22 ) M 7 = ( A 11 − A 21 ) ( B 11 + B 12 ) ⟹ C 11 = M 4 + M 5 + M 6 − M 2 C 12 = M 1 + M 2 C 21 = M 3 + M 4 C 22 = M 1 + M 5 − M 3 − M 7
\begin{matrix}
M_1=A_{11}(B_{12}-B_{22})\\
M_2=(A_{11}+A_{12})B_{22}\\
M_3=(A_{21}+A_{22})B_{11}\\
M_4=A_{22}(B_{21}-B_{11})\\
M_5=(A_{11}+A_{22})(B_{11}+B_{22})\\
M_6=(A_{12}-A_{22})(B_{21}+B_{22})\\
M_7=(A_{11}-A_{21})(B_{11}+B_{12})
\end{matrix}
\implies
\begin{matrix}
C_{11}=M_4+M_5+M_6-M_2\\
C_{12}=M_1+M_2\\
C_{21}=M_3+M_4\\
C_{22}=M_1+M_5-M_3-M_7
\end{matrix}
M 1 = A 1 1 ( B 1 2 − B 2 2 ) M 2 = ( A 1 1 + A 1 2 ) B 2 2 M 3 = ( A 2 1 + A 2 2 ) B 1 1 M 4 = A 2 2 ( B 2 1 − B 1 1 ) M 5 = ( A 1 1 + A 2 2 ) ( B 1 1 + B 2 2 ) M 6 = ( A 1 2 − A 2 2 ) ( B 2 1 + B 2 2 ) M 7 = ( A 1 1 − A 2 1 ) ( B 1 1 + B 1 2 ) ⟹ C 1 1 = M 4 + M 5 + M 6 − M 2 C 1 2 = M 1 + M 2 C 2 1 = M 3 + M 4 C 2 2 = M 1 + M 5 − M 3 − M 7
算法复杂度分析:T ( n ) = { O ( 1 ) n = 2 8 T ( n / 2 ) + O ( n 2 ) n > 2 T(n)=
\begin{cases}
O(1)\ n=2\\
8T(n/2)+O(n^2)\ n>2
\end{cases} T ( n ) = { O ( 1 ) n = 2 8 T ( n / 2 ) + O ( n 2 ) n > 2
T ( n ) = O ( n l o g 7 ) = O ( n 2.81 ) T(n)=O(n^{log7}) =O(n^{2.81}) T ( n ) = O ( n l o g 7 ) = O ( n 2 . 8 1 )
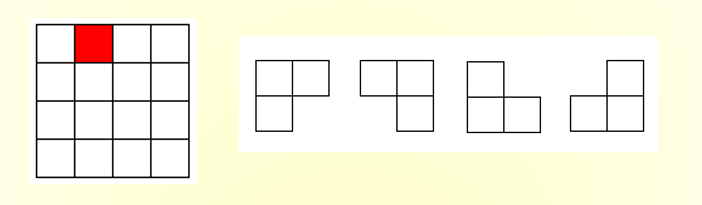
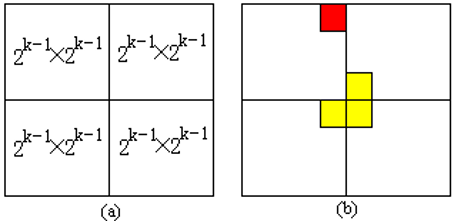
# 棋盘覆盖在一个2 k × 2 k 2^k×2^k 2 k × 2 k
当 k>0 时,将2 k × 2 k 2^k×2^k 2 k × 2 k 2 k − 1 × 2 k − 1 2^{k-1}×2^{k-1} 2 k − 1 × 2 k − 1
棋盘覆盖 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 void chessBoard (int tr, int tc, int dr, int dc, int size) { if (size == 1 ) return ; int t = tile++, s = size/2 ; if (dr < tr + s && dc < tc + s) chessBoard(tr, tc, dr, dc, s); else { board[tr + s - 1 ][tc + s - 1 ] = t; chessBoard(tr, tc, tr+s-1 , tc+s-1 , s);} if (dr < tr + s && dc >= tc + s) chessBoard(tr, tc+s, dr, dc, s); else { board[tr + s - 1 ][tc + s] = t; chessBoard(tr, tc+s, tr+s-1 , tc+s, s);} if (dr >= tr + s && dc < tc + s) chessBoard(tr+s, tc, dr, dc, s); else { board[tr + s][tc + s - 1 ] = t; chessBoard(tr+s, tc, tr+s, tc+s-1 , s);} if (dr >= tr + s && dc >= tc + s) chessBoard(tr+s, tc+s, dr, dc, s); else { board[tr + s][tc + s] = t; chessBoard(tr+s, tc+s, tr+s, tc+s, s);} }
算法复杂度分析:
T ( k ) = { O ( 1 ) k = 0 4 T ( k − 1 ) + O ( 1 ) k > 0 T(k)=\begin{cases}
O(1)\ k=0\\
4T(k-1)+O(1)\ k>0
\end{cases} T ( k ) = { O ( 1 ) k = 0 4 T ( k − 1 ) + O ( 1 ) k > 0
T ( n ) = O ( 4 k ) T(n)=O(4^k) T ( n ) = O ( 4 k )
# 合并排序将待排序元素分成大小大致相同的 2 个子集合,分别对 2 个子集合进行排序,最终将排好序的子集合合并成为所要求的排好序的集合
合并排序 1 2 3 4 5 6 7 8 9 10 void MergeSort (Type a[], int left, int right) { if (left<right) { int i=(left+right)/2 ; mergeSort(a, left, i); mergeSort(a, i+1 , right); merge(a, b, left, i, right); copy(a, b, left, right); } }
算法复杂度分析:T ( n ) = { O ( 1 ) n ≤ 1 2 T ( n / 2 ) + O ( n ) n > 1 T(n)=\begin{cases}
O(1)\ n\leq1\\
2T(n/2)+O(n)\ n>1
\end{cases} T ( n ) = { O ( 1 ) n ≤ 1 2 T ( n / 2 ) + O ( n ) n > 1 T ( n ) = O ( n l o g n ) T(n)=O(nlogn) T ( n ) = O ( n l o g n )
# 快速排序在快速排序中,记录的比较和交换是从两端向中间进行的,关键字较大的记录一次就能交换到后面单元,关键字较小的记录一次就能交换到前面单元,记录每次移动的距离较大,因而总的比和移动次数较少。
快速排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 template<class Type > void QuickSort (Type a[], int p, int r) { if (p<r) { int q=Partition(a,p,r); QuickSort (a,p,q-1 ); QuickSort (a,q+1 ,r); } } template<class Type > int Partition (Type a[], int p, int r) { int i = p, j = r + 1 ; Type x=a[p]; while (true ) { while (a[++i] <x); while (a[- -j] >x); if (i >= j) break ; Swap(a[i], a[j]); } a[p] = a[j]; a[j] = x; return j; }
快速排序算法的性能取决于划分的对称性。通过修改算法 partition,可以设计出采用随机选择策略的快速排序算法。在快速排序算法的每一步中,当数组还没有被划分时,可以在 a [p:r] 中随机选出一个元素作为划分基准,这样可以使划分基准的选择是随机的,从而可以期望划分是较对称的。
改进 1 2 3 4 5 6 7 template<class Type > int RandomizedPartition (Type a[], int p, int r) { int i = Random(p,r); Swap(a[i], a[p]); return Partition (a, p, r); }
最坏时间复杂度:O (n2)
# 线性时间选择给定线性序集中 n 个元素和一个整数 k,1≤k≤n,要求找出这 n 个元素中第 k 小的元素
线性时间选择 1 2 3 4 5 6 7 8 9 template<class Type > Type RandomizedSelect (Type a[],int p,int r,int k) { if (p==r) return a[p]; int i=RandomizedPartition(a,p,r), j=i-p+1 ; if (k<=j) return RandomizedSelect(a,p,i,k); else return RandomizedSelect(a,i+1 ,r,k-j); }
在最坏情况下,算法 randomizedSelect 需要O ( n 2 ) O(n^2) O ( n 2 ) O ( n ) O(n) O ( n )
将 n 个输入元素划分成⌈ n / 5 ⌉ \lceil n/5 \rceil ⌈ n / 5 ⌉ ⌈ n / 5 ⌉ \lceil n/5 \rceil ⌈ n / 5 ⌉
递归调用 select 来找出这⌈ n / 5 ⌉ \lceil n/5 \rceil ⌈ n / 5 ⌉ ⌈ n / 5 ⌉ \lceil n/5 \rceil ⌈ n / 5 ⌉
线性时间选择 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Type Select (Type a[], int p, int r, int k) { if (r-p<75 ) { 用某个简单排序算法对数组a[p:r]排序; return a[p+k-1 ]; }; for ( int i = 0 ; i<=(r-p-4 )/5 ; i++ ) 将a[p+5 *i]至a[p+5 *i+4 ]的第3 小元素 与a[p+i]交换位置; Type x = Select(a, p, p+(r-p-4 )/5 , (r-p-4 )/10 ); int i=Partition(a,p,r, x), j=i-p+1 ; if (k<=j) return Select(a,p,i,k); else return Select(a,i+1 ,r,k-j); }
上述算法将每一组的大小定为 5,并选取 75 作为是否作递归调用的分界点。这 2 点保证了 T (n) 的递归式中 2 个自变量之和 n/5+3n/4=19n/20=εn,0<ε<1。这是使 T (n)=O (n) 的关键之处。当然,除了 5 和 75 之外,还有其他选择。
算法复杂度分析:T ( n ) ≤ { C 1 n < 75 C 2 n + T ( n / 5 ) + T ( 3 n / 4 ) n ≥ 75 T(n)\leq \begin{cases}
C_1\ n<75\\
C_2n+T(n/5)+T(3n/4)\ n\geq 75
\end{cases} T ( n ) ≤ { C 1 n < 7 5 C 2 n + T ( n / 5 ) + T ( 3 n / 4 ) n ≥ 7 5 T ( n ) = O ( n ) T(n)=O(n) T ( n ) = O ( n )
# 线性时间选择的个人理解
首先将整个数组每五个为一组划分,找到每一组的中位数,并将中位数交换至数组头部.
由于每组的中位数都在数组头部,再次调用函数求头部的 n/5 个数字当中的中位数,设为 x;
只要能对这几个中位数进行操作求得中位数的中位数即可,交换与否,交换的位置影响不大.
使用 partition 函数,数组中小于 x 的放左边,大于 x 的放右边.
核心思路依然是取一个值,然后分隔数组,但花费了不少时间来找到这个合适的值.
由于分出了 n/5 个组,在每个组求中位数的过程中,花销为 T (5)*n/5=cn.
求每个组的中位数的中位数过程中,花销为 T (n/5).
求得的这个新的中位数,他要比 (n/5-1)/2 个其他中位数要小,每个组内还有两个数比组内中位数大,那么就有 3 (n/5-1)/2 个数比 x 大,也就是3 ( n − 5 ) / 10 ≥ n / 4 3(n-5)/10\geq n/4 3 ( n − 5 ) / 1 0 ≥ n / 4
由于 3n/4+n/5 小于 n, 这个算法就能降低复杂度
# 最接近点对问题二维空间内有若干个点,寻找其中最接近的两个点
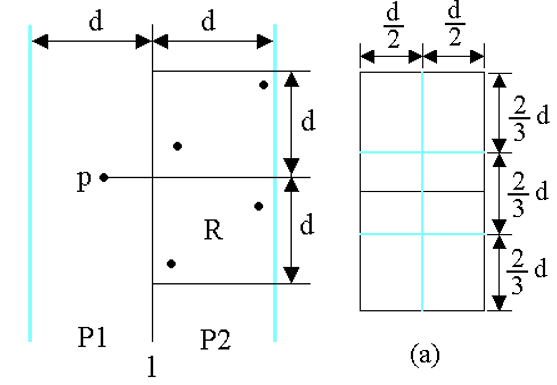
选取一垂直线 l:x=m 来作为分割直线。其中 m 为 S 中各点 x 坐标的中位数。由此将 S 分割为 S1 和 S2。
递归地在 S1 和 S2 上找出其最小距离 d1 和 d2,并设 d=min {d1,d2},S 中的最接近点对或者是 d,或者是某个 {p,q},其中 p∈P1 且 q∈P2。
考虑 P1 中任意一点 p,它若与 P2 中的点 q 构成最接近点对的候选者,则必有 distance (p,q)<d。满足这个条件的 P2 中的点一定落在一个 d×2d 的矩形 R 中
由 d 的意义可知 (d=min {d1,d2}),P2 中任何 2 个 S 中的点的距离都不小于 d。由此可以推出矩形 R 中最多只有 6 个 S 中的点。
因此,在分治法的合并步骤中最多只需要检查 6×n/2=3n 个候选者
证明:将矩形 R 的长为 2d 的边 3 等分,将它的长为 d 的边 2 等分,由此导出 6 个 (d/2)×(2d/3) 的矩形。若矩形 R 中有多于 6 个 S 中的点,则由鸽舍原理易知至少有一个 (d/2)×(2d/3) 的小矩形中有 2 个以上 S 中的点。设 u,v 是位于同一小矩形中的 2 个点,则( x ( u ) − x ( v ) ) 2 + ( y ( u ) − y ( v ) ) 2 ≤ ( d / 2 ) 2 + ( 2 d / 3 ) 2 = 25 36 d 2 (x(u)-x(v))^2+(y(u)-y(v))^2\leq (d/2)^2+(2d/3)^2=\frac{25}{36}d^2 ( x ( u ) − x ( v ) ) 2 + ( y ( u ) − y ( v ) ) 2 ≤ ( d / 2 ) 2 + ( 2 d / 3 ) 2 = 3 6 2 5 d 2
为了确切地知道要检查哪 6 个点,可以将 p 和 P2 中所有 S2 的点投影到垂直线 l 上。由于能与 p 点一起构成最接近点对候选者的 S2 中点一定在矩形 R 中,所以它们在直线 l 上的投影点距 p 在 l 上投影点的距离小于 d。由上面的分析可知,这种投影点最多只有 6 个。
因此,若将 P1 和 P2 中所有 S 中点按其 y 坐标排好序,则对 P1 中所有点,对排好序的点列作一次扫描,就可以找出所有最接近点对的候选者。对 P1 中每一点最多只要检查 P2 中排好序的相继 6 个点。
最接近点对问题 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 double cpair2 (S) { n=|S|; if (n < 2 ) return ; 1 、m=S中各点x间坐标的中位数; 构造S1和S2; S2={p∈S|x(p)>m} 2 、d1=cpair2(S1); d2=cpair2(S2); 3 、dm=min(d1,d2);4 、设P1是S1中距垂直分割线l的距离在dm之内的所有点组成的集合; P2是S2中距分割线l的距离在dm之内所有点组成的集合; 将P1和P2中点依其y坐标值排序; 并设X和Y是相应的已排好序的点列; 5 、通过扫描X以及对于X中每个点检查Y中与其距离在dm之内的所有点(最多6 个)可以完成合并; 当X中的扫描指针逐次向上移动时,Y中的扫描指针可在宽为2dm的区间内移动; 设dl是按这种扫描方式找到的点对间的最小距离; 6 、d=min(dm,dl); return d; }
算法复杂度分析:T ( n ) ≤ { O ( 1 ) n < 4 2 T ( n / 2 ) + O ( n ) n ≥ 4 T(n)\leq \begin{cases}
O(1)\ n<4\\
2T(n/2)+O(n)\ n\geq 4
\end{cases} T ( n ) ≤ { O ( 1 ) n < 4 2 T ( n / 2 ) + O ( n ) n ≥ 4 T ( n ) = O ( n l o g n ) T(n)=O(nlogn) T ( n ) = O ( n l o g n )
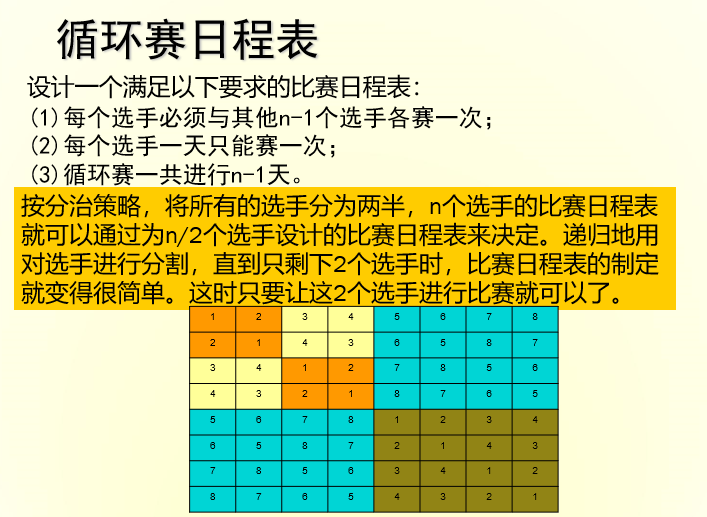
# 循环赛程表